From Integers to Rings and Ideals: An Introduction to Algebraic Number Theory

One of the key ways mathematics progresses is by first identifying a pattern in a more-or-less familiar setting, and then taking a leap by trying to extend this pattern to a more general environment—one that is, in some sense, larger than the previous one. Perhaps the old pattern still holds, or perhaps it doesn’t. In the latter case, our goal is to understand exactly where, in the leap of abstraction, it fails. Usually, the by-product of this process is the creation of an entirely new landscape of mathematical objects. On the one hand, these objects follow certain intuitive rules inherited from our original setting; on the other hand, they introduce fundamentally new structures. At any rate, the motto here is: with generalization, through abstraction, comes power—as we shall explore today.

The Integers: Our First Abstraction

Our story begins with the integers (denoted here by $\mathbb{Z}$ ), which are essentially the numbers you will recite as you count the hairs on your head or the grains of sand on a beach—along with their negatives. Another way to think about them is to draw them against the backdrop of the continuum of real numbers (or simply a line, which is what the real numbers are!). They appear like a one-dimensional version of galaxies in the universe against the vacuum of space: evenly spaced and discrete, like a sieve. After all, there are no integers between, say, $0$ and $1$ , whereas there are an awful lot of real numbers—infinite decimals—between $0$ and $1$ ! In fact, there are so many real numbers (no matter how far you zoom into the number line, you just keep seeing more) that we cannot even count them — but that is a story for another day.

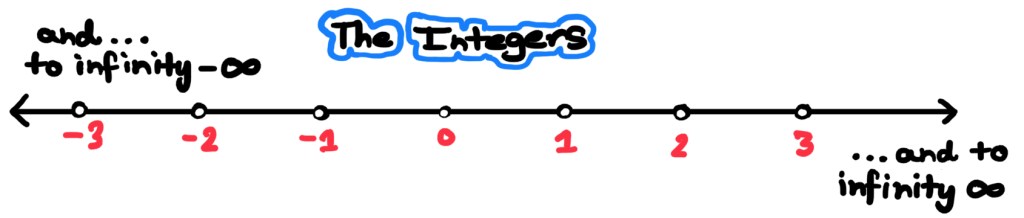
The integers aren’t terribly exciting just sitting there like dots, staring up at us – and they weren’t invented to just stay put anyways! Indeed, their raison d’être is to do calculations – like after measuring the length and breadth of a plot of land, say $120$ meters and $67$ meters, we would multiply the two numbers up to get the area of the plot – the number of tiny $1$ meter by $1$ meter squares that make up the entirety of the humungous plot. And we even developed a fool-proof algorithm to multiply two integers like $120$ and $67$ , something we learnt way back in elementary school! Notice that if I had to figure out, say, the money I would earn if I sold $120$ of my hairs for $67$ dollars each (yuck!), I would do the exact same thing, even though a huge amount of dirt (that is, the plot) and dead cells (that is, my hair) are nowhere near to being equal!

And just like that, we have our first, albeit painfully trivial, abstraction, a thing that is strewn in such high quantities across the mathematical landscape that it practically makes it up. The number $120$ is a clean ‘abstraction’, meant to represent $120$ hairs and $120$ meters of dirt at the same time! We created the integers as a whole by observing a specific commonality between two very distinct sets of objects – their number!

The next step after getting rid of all the unnecessary details (In the context of counting, this was simply replacing each instance of that particular object with the same indistinguishable token, so that only differences in the number count, as opposed to a difference in structure or the appearance. At other times, we may be interested in other properties of objects, so that we abstract differently — keep this in mind!) to create a set of ‘counting classes’, is to formulate meaningful rules to manipulate these ‘counting classes’. As we saw, thanks to the reasonably large degree of abstraction that went into creating the integers — in that one integer can stand for a frighteningly large diversity of objects — in the first place, these rules will carry quite a bit of power.

One such rule is multiplication: On one level, it’s just a procedure to convert an input of two integers into a single one (one of infinitely many so-called binary operations — try inventing a few yourself!), but it is deeply grounded in a concrete physical meaning — the area of a rectangle — as we saw. The other main rule is that of addition, which has a yetmore elementary physical interpretation: the total number of objects when many collections of objects are placed side-by-side. The last step, obviously, is to interpret the result of the abstract manipulation in the context of the situation!

Taking Off

Now, we play around with the integers, building up to our central characters — a very special subset of the integers.

You might notice that given integer $1$ and the operation $+$ , you can reach any positive integer: $2 = 1 + 1$ , $3 = 1 + 1 + 1$ and so on (we’re ignoring the negatives and zero for the moment), but that $1$ and $\times$ keeps you firmly stuck on $1$ . Indeed, no single number and $\times$ can create the whole of $\mathbb{Z}^+$ (the set of positive integers). Instead we must broaden our scope and ask what subset $S$ of the integers along with $\times$ can generate $\mathbb{Z}^+$ ? Clearly we can choose $S = \mathbb{Z}$ , so we really should be asking for the smallest possible $S$ . In some sense, $S$ compressesdown $\mathbb{Z}$ under multiplication as much as possible!

One way to think about this is to first restrict our field of vision down to the set , and then increasing it to and then to , continuing on like this, just adding one number at a time, building for each of these restricted versions of . You can think about the greatest element of this chain of sets like a slider, and we’re pulling it out to infinity, a step at a time. We shall use to denote the for .

First, for , is just the whole thing: you need both and , as we noted above. Second, we consider . There too, you realize that you need as well, as multiplying by itself and by any number of times is always even, and is odd: so , where we added that little to denote the set of all numbers you can get by multiplying and with each other any number of times. Observe that is always contained in .

This pattern halts, at least for once, at the third set: . Here you do not need to add to , as , meaning that . For the first time, we’ve been able to truly compress such a set, albeit to a very small degree! Try computing more ‘s!

As you might’ve already guessed, is essentially the set of the so-called prime numbers: the building blocksof the integers under multiplication, or the most compressed version of the integers under multiplication, as we have just seen. The other elements of (the elements of the set theoretic difference ), the compressible numbers, are called composite numbers.

A playful analogy to draw here (and one that we will come back to surprisingly often) is to think of the primes as atomsand composite numbers like molecules from chemistry (we are not assigning primes to quarks for a very deliberate reason!). This analogy has many limitations, one of them being that prime numbers are infinite in number, whereas there are only finitely many stable atoms, but let us overlook these transactional details for the moment.

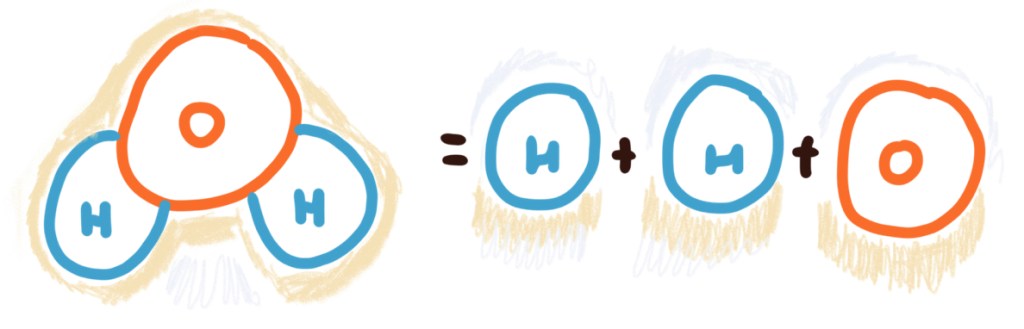
Indeed, this connection helps us come to terms with a notable property of the integers, that of unique factorization. Take the example of a molecule of water — essentially an oxygen atom stuck (the analogue of multiplication) to two hydrogen atoms. Notice that a water molecule will only ever be made up of atoms in this particular way: one atom connected to two atoms! Drawing on this analogy, it would seem only logical for this to hold in as well: in that every integer can be expressed uniquely as the product of primes — the composite number 105 is and is only . And, as it turns out, it does actually hold!

Water is, and is always going to be, H+H+O.

But this is not always true—only when we are naive and narrow-minded.

What’s Next?

Less abstractly, we’re going to move beyond the realm of the usual integers, creating new, integer like objects (mind you, there are not the integers, only similar), where the same element has two different prime factorizations—loss of unique factorization! These integer like objects will live in the complex plane, rather than the real line, as you shall soon see. Then, in an attempt to recover unique factorization in this new setting, we will find ourselves replacing individual numbers, with sets of numbers—and so we will succeed in creating a new object as a result of trying to extend a broken pattern.

Before we set (pun intended!) out on our adventure to foreign landscapes, let us take one last look at divisibility in —which will give a hint at those ‘sets’ we’ll ultimately be considering.

Divisibility and Sets

When we say divides (written as ) what do we mean? On the one hand, it is simply saying that is an integer, as opposed to a fraction or even worse, a real number (formally, there exists an integer such that )—but there’s also a visual way to analyse this situation.

We start with the integers—evenly spaced and looking up at us as usual—and stretch on them, keeping fixed, so that the distances between next-door integers increase by a factor of : is now where was and is where was. If we remove the labels on the dots and place this transformed line atop the original one, we see we’re left with $2$ ’ s version of the integers: the integers you’d be able to visit if you only were armed with a pair of self-regenerating arrows: one that read ‘JUMP $+2$ ’ and another that read ‘JUMP $-2$ ’. In fact, this is a way to view the integer as acting upon : it yields the set—really a proxy of the integers—, the set of all multiples of .

2’s version of the integers.

Now, what happens when we place $4$ ’s version of the integers upon $2$ ’s version of the integers? Didn’t notice? Well, try reversing the order by first placing $4$ ’s version of the integers on the base slate and then placing $2$ ’s version of the integers atop that. Did you see what happened? $4$ ’s version of the integers was completely and cleanly masked by $2$ ’s version of the integers! Mathematically, the set $4$ ’s version of the integers is contained in the set $2$ ’s version of the integers.

This is because the new pairs of arrows—one created by gluing two ‘JUMP $+2$ ’ arrows and the other created by gluing two ‘JUMP $-2$ ’ arrows—mean you can visit even fewer integers than before: you’ve surrendered your precise visiting abilities! Essentially, this clean containment of sets is a manifestation of the fact that $2$ divides $4$ —try and see this!

4’s version of the integers.

On the other hand, the result is not so satisfying if we place $3$ ’s version of the integers atop $2$ ’s version of the integers or the other way. We don’t get a clean containment—we can see orange and red dots lurking here and there. This is precisely because does not divide . Indeed, $n$ ’s version of the integers is always contained in —which is $1$ ’s version of the integers—because every integer is divisible by .

To sum up, we can view a single integer as a set—its version of the integers, which is its multiples—and divisibility can be seen as a containment of those sets.

And now, we create our new integers.

Travelling Beyond

Let’s take another look at , this time with their ambient space in mind—the real numbers, which is essentially a line, a one-dimensional object. Could we come up with an analogue of the integers for a plane rather than a line? That object would truly earn the moniker of a sieve.

Well, mathematically speaking, the complex numbers describe a plane, just like how the real numbers describe a line. As a review, the complex numbers is the set , which can alternatively be viewed as ordered pairs of real numbers, along with well-defined rules for addition, subtraction, multiplication, and division. The most natural notion of an integer here would be a complex number where both the real and imaginary parts are integers: geometrically, you’re starting with the usual integers and translating them upwards and downwards in the complex plane by an integer.

We’ll use to denote this notion of the complex integers (notation to be explained!). And sure enough, the picture looks pretty convincing—equally spaced dots looking up at us!

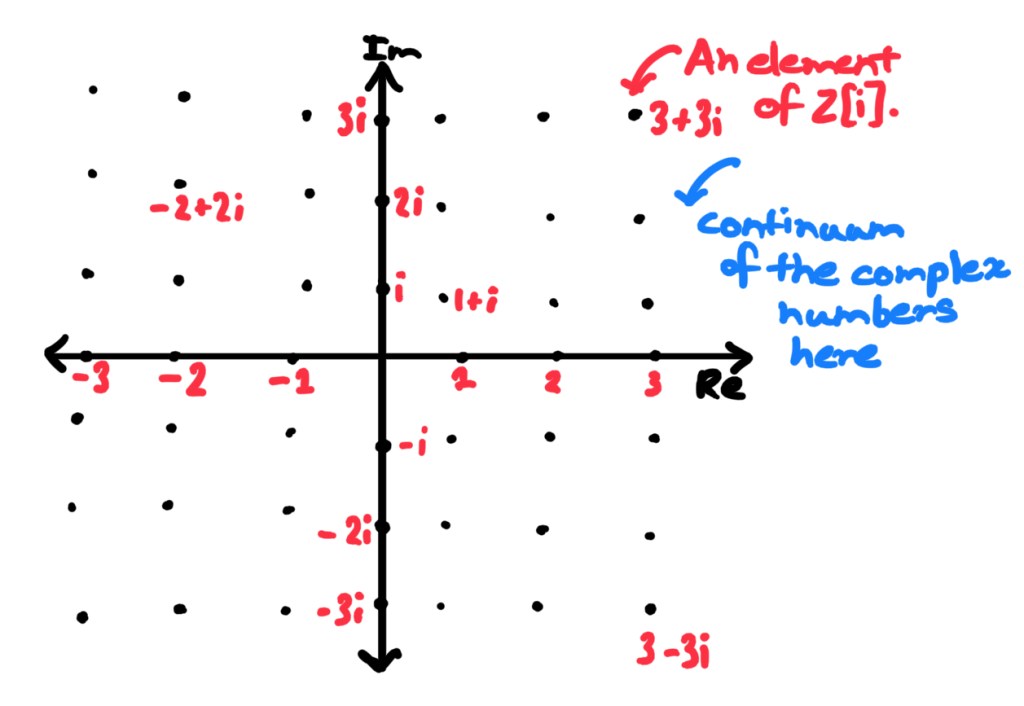
What’s more is that one can still add, subtract, and multiply any two such elements of and get back an element of , but you can’t necessarily divide, in the sense that the quotient of two such elements need not be in —just like it was in ! Try and find examples of such quotients! Recall that it was precisely because of the fact that you can’t cleanly divide any two integers that it made sense or was non-trivial to talk about divisibility (anything divides into anything in , anything divides into anything in ).

To make things seem a bit less abstract, let’s actually write down the rules for the arithmetic operations on . How do we add and ? Just like we add complex numbers! After all, and are complex numbers—just like how adding two integers, say and , is the same as adding the real numbers and .

Explicitly,

$(a+bi)+(c+di)=(a+c)+i(b+d)$ .

This sum is in because , the real part, and , the imaginary part, are both integers—as and are integers, and an integer plus another integer is an integer! A very similar analysis can be done for multiplication!

But this is naive thinking as well. Instead of translating the integers upwards and downwards by an integer, why not by an integral multiple of ?

Check it out! This picture also looks pretty convincing!

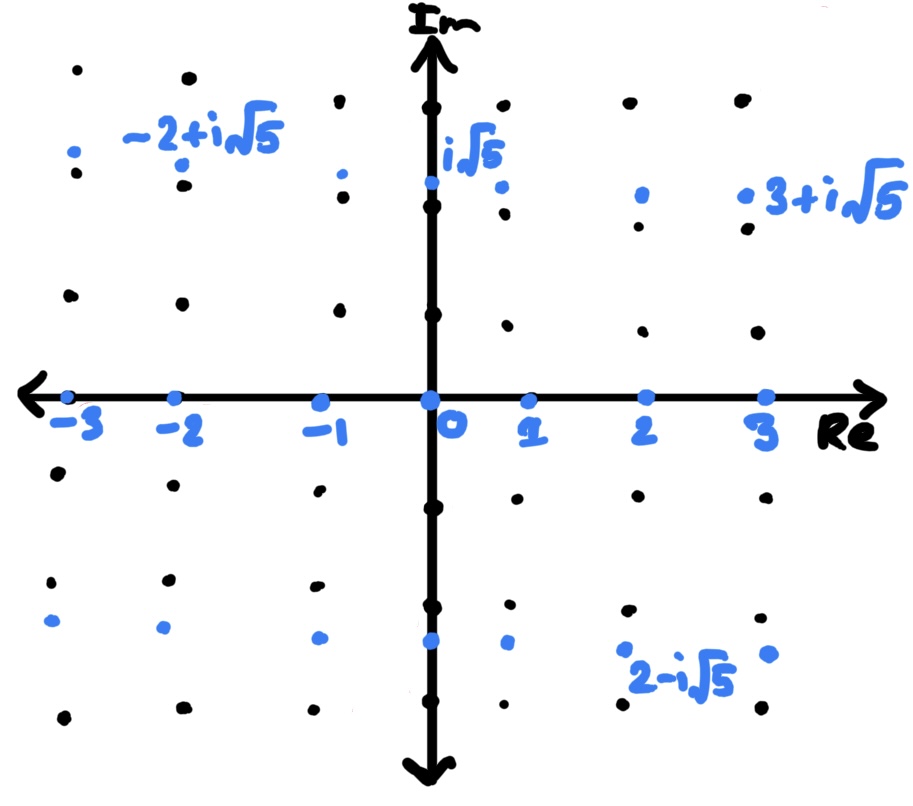
*The new version of the complex integers. The elements of this set are colored blue, while the orginal complex integers are black.*

Another way to think about it is we’ve applied the transformation represented by the matrix:

$\begin{bmatrix}1 & 0 \\0 & \sqrt{5}\end{bmatrix}$

to each element of . We’ll denote this set by (can you guess what the notation means?). Written down explicitly, we start with an integer , and translating it upwards/downwards by an integral multiple of is the same thing as adding for some integer (the degree of translation) to —so: $\mathbb{Z}[i\sqrt{5}] = \{a + bi\sqrt{5} : a, b \in \mathbb{Z}\}$ . Essentially, we’ve just multiplied the vector with the matrix above.

What’s more—you can probably guess what’s going to happen—we can still add, subtract, and multiply elements of and get back an element of —try verifying this! And then, again, you can’t always divide in , so we can talk about divisibility here as well!

The astute readers among you may not be quite convinced—yes, is great, but why did we have to stretch in the y-direction only? We could have done the same thing with the horizontal axis, stretching it out by a factor of , say?

And we could have completely done that—that set would still look discrete (try drawing a picture), and still have the basic arithmetic operations apart from division. The only problem with that would be that we would inadvertently lose —the multiplicative identity—in the process, and we kind of want that number to be around, as it was present in . Stretching in the vertical direction allows us to keep , lying on the horizontal axis, intact.

Where are the Primes?

Before we can start doing some factorization in these new lands, as promised, we need to recover the notion of a prime. What does it mean for an element of $\mathbb{Z}[i]$ or $\mathbb{Z}[i\sqrt{5}]$ to be a prime? To answer that, we ask what does it mean for an element of $\mathbb{Z}$ to be prime?

Well, it’s a usual integer $p$ such that its only divisors are $+1$ , $-1$ , $+p$ and $-p$ . Phrased differently, it’s a number $p$ such that if we write $p = ab$ where $a$ and $b$ are integers, then one of them must be $+1$ or $-1$ . Essentially, only trivial divisors are allowed to divide that number, not even a peep more—and we will be using this exact definition in $\mathbb{Z}[i]$ and $\mathbb{Z}[i\sqrt{5}]$ .

Except that there are more trivial divisors—numbers that divide every element—than just $+1$ and $-1$ here! But what are they?

Let’s stick with $\mathbb{Z}[i]$ first. Clearly $+1$ and $-1$ work, because their version of $\mathbb{Z}[i]$ —their multiples in $\mathbb{Z}[i]$ —is the whole of $\mathbb{Z}[i]$ . And why is that? Because they are the closest to $0$ as possible—their step size, their arrow propels one forward as little as possible each time it is thrown. In particular, they are a unit distance away from the origin. Similarly, $+i$ and $-i$ are also a distance of $1$ from the origin, and they divide every complex number as well!

All in all, it can be shown that the four numbers $-1$ , $1$ , $-i$ , $i$ are the only trivial divisors! Any other number will not work because it is too far.

There is a way to see this purely algebraically as well: we are looking for $a + bi \in \mathbb{Z}[i]$ such that the quotient $(c + di) / (a + bi)$ lies in $\mathbb{Z}[i]$ for all $c + di \in \mathbb{Z}[i]$ . That is, $a + bi$ divides all $c + di$ . Notice that this necessarily means that $(a + bi)^{-1}$ must be a complex integer, simply by setting $c + di = 1$ . Conversely, if $a + bi$ has a multiplicative inverse (that is, $(a + bi)^{-1}$ ) in $\mathbb{Z}[i]$ , then the quotient

$\frac{a+bi}{c+di}=(a+bi)(c+di)^{-1},$

is automatically in $\mathbb{Z}[i]$ for all $c + di$ ! An element is a trivial divisor precisely when it is invertible!

Next, we massage the expression for $(a + bi)^{-1}$ a bit, by realizing the denominator:

$\frac{1}{a+bi}\times \frac{a-bi}{a-bi}=\frac{a-bi}{a^2+b^2}$

Recall that both the real and imaginary parts must be integers, so that $a^2 + b^2$ must divide $a$ and also divide $b$ . Try and see if you can complete this argument!

We can do something similar in $\mathbb{Z}[i\sqrt{5}]$ . There, the only such numbers are the old $-1$ and $+1$ —you might be tempted by $i\sqrt{5}$ , but it is too far from $0$ . Indeed, $1$ is not even present in $i\sqrt{5}$ ‘s version of the integers as it is too close to $0$ .

We call $-1$ , $1$ , $i$ , $-i$ the units of $\mathbb{Z}[i]$ , and $-1$ , $1$ the units of $\mathbb{Z}[i\sqrt{5}]$ —named quite naturally! And now we can define the analogue of primes in $\mathbb{Z}[i]$ : the same definition holds for $\mathbb{Z}[i\sqrt{5}]$ .

We say that an element $x$ of $\mathbb{Z}[i]$ is irreducible, if whenever we write $x$ as the product of two elements in $\mathbb{Z}[i]$ , one of them is a unit.

And now we factorize $6$ —quite a benign number, to say the least—in $\mathbb{Z}[i\sqrt{5}]$ .

The Breaking Point

Well, we all know that $6 = 2 \times 3$ . But now we’re talking in $\mathbb{Z}[i\sqrt{5}]$ , so we have more exotic looking factorizations. In fact, notice that $6 = (1 + i\sqrt{5})(1 - i\sqrt{5})$ , and so

$6 = 2 \times 3 = (1 + i\sqrt{5})(1 - i\sqrt{5}).$

This might hardly seem surprising. After all, there are so many ways to write a regular integer as a product—as a baby example take $24 = 2 \times 12 = 4 \times 6$ .

But, in this case, all the involved $6$ -invited partygoers— $2, 3, 1 + i\sqrt{5}, 1 - i\sqrt{5}$ —are irreducibles—not a casual $4$ , $6$ , $12$ or $24$ strolling down composite avenue nonchalantly.

“No way!” you shout! How can that be? $2$ and $3$ may be irreducibles, but $1 + i\sqrt{5}$ ? Seriously? I mean it literally comes in two parts!

But all we have to do is appeal to our freshly baked definition about irreducible—if $1 + i\sqrt{5}$ is really an irreducible, then whenever we write $1 + i\sqrt{5} = \alpha \beta$ for some $\alpha$ and $\beta$ in $\mathbb{Z}[i\sqrt{5}]$ , then at least one of them— $\alpha$ or $\beta$ —must be $-1$ or $+1$ , and if that turns out to be true, case closed!

First, let’s expand $\alpha$ and $\beta$ a bit. Leveraging the set-theoretic definition of $\mathbb{Z}[i\sqrt{5}]$ , we can write $\alpha = a + b i \sqrt{5}$ and $\beta = c + d i \sqrt{5}$ , for some integers $a, b, c$ and $d$ . Putting everything together,

$1 + i \sqrt{5} = (a + b i \sqrt{5})(c + d i \sqrt{5}).$

Now, we could expand the right side, but that is likely to get messy. Instead, we simply take the usual complex number absolute value of both sides,

$|1 + i \sqrt{5}| = \sqrt{6} = |a + b i \sqrt{5}| \times |c + d i \sqrt{5}| = \sqrt{a^2 + 5 b^2} \sqrt{c^2 + 5 d^2}.$

We don’t want those pesky square roots, so we simply square both sides to get

$6 = (a^2 + 5 b^2)(c^2 + 5 d^2).$

Notice that both terms on the right side are usual integers, and the left side is obviously an integer—and so from an equation involving elements in $\mathbb{Z}[i\sqrt{5}]$ we have an equation entirely in the integers!

Remember what we want to do: show that one of $\alpha = a + b i \sqrt{5}$ or $\beta = c + d i \sqrt{5}$ must be an integer. Well, on the one hand $6$ is the product of the two integers $a^2 + 5 b^2$ and $c^2 + 5 d^2$ , and on the other hand, can only be written as $6 \times 1$ or $2 \times 3$ as a product of two (positive) integers! So, $a^2 + 5 b^2$ and $c^2 + 5 d^2$ must be one of $1, 2, 3$ or $6$ . Let’s go case by case!

If $a^2 + 5 b^2 = 1$ then we’re done— $a$ must be one and $b$ must be zero, meaning that $\alpha = 1$ (see why this is the case!). Similarly, if $a^2 + 5 b^2 = 6$ , then the other factor, $c^2 + 5 d^2$ must be $1$ , meaning that $\beta = 1$ this time.
Next, consider $a^2 + 5 b^2 = 3$ . This is simply not possible, as $5 b^2$ is too large to be $3$ —it is always greater than $3$ for non-zero $b$ , meaning that if this equation were to have a solution, then $b$ must be $0$ . In that case, $a^2 = 3$ , but $3$ is not even rational, so no integer $a$ exists. Similarly, one can show that $a^2 + 5 b^2 = 2$ is not possible.

Phew! That was some algebra heavy-lifting! But at the end of the day, look what we have— $1 + i \sqrt{5}$ is an irreducible in $\mathbb{Z}[i\sqrt{5}]$ ! And in much the same way, its partner in crime, $1 - i \sqrt{5}$ is also an irreducible. All in all,

$6 = \textrm{Irreducible} \times \textrm{Irreducible} = \textrm{Different Irreducible} \times \textrm{Different Irreducible},$

something hard to reconcile with our experience in $\mathbb{Z}$ !

And with that, we transition into rescue mode. Can we, in some way, recover unique factorization in this new set-up?

Try Hard Enough and…

Kummer, a German mathematician, would have none of this corrupt, $\mathbb{Z}[i\sqrt{5}]$ -unacceptable business. The way he saw it, we ended up in such a weird situation simply because we hadn’t factored enough.

Taking this thought quite literally, his idea was to have ‘numbers’ – notice the quotation marks – $\mathfrak{a}_1$ , $\mathfrak{a}_2$ , $\mathfrak{a}_3$ and $\mathfrak{a}_4$ such that $2 = \mathfrak{a}_1 \times \mathfrak{a}_2$ and $3 = \mathfrak{a}_3 \times \mathfrak{a}_4$ on the one side; and on the other side, $1 + i \sqrt{5} = \mathfrak{a}_1 \times \mathfrak{a}_3$ and $1 - i \sqrt{5} = \mathfrak{a}_2 \times \mathfrak{a}_4$ .

Now, on the one hand

$6 = 2 \times 3 = (\mathfrak{a}_1 \times \mathfrak{a}_2) \times (\mathfrak{a}_3 \times \mathfrak{a}_4) = \mathfrak{a}_1 \times \mathfrak{a}_2 \times \mathfrak{a}_3 \times \mathfrak{a}_4,$

and on the other hand

$6 = (1 + i \sqrt{5}) \times (1 - i \sqrt{5}) = (\mathfrak{a}_1 \times \mathfrak{a}_3) \times (\mathfrak{a}_2 \times \mathfrak{a}_4) = \mathfrak{a}_1 \times \mathfrak{a}_2 \times \mathfrak{a}_3 \times \mathfrak{a}_4,$

which would avoid all the drama! But what are these mysterious characters? Surely they can’t be numbers – elements of $\mathbb{Z}[i\sqrt{5}]$ ! Indeed: Kummer merely hoped that playing around with these $\mathfrak{a}$ ‘s might lead to some deeper insights.

Let’s start by focusing on $\mathfrak{a}_1$ . First, $\mathfrak{a}_1 \times \mathfrak{a}_2 = 2$ , so $\mathfrak{a}_1$ divides $2$ . Well, then $\mathfrak{a}_1$ must divide any multiple of two – just like how $2 \mid 4 \implies 2 \mid 4n$ for any $n \in \mathbb{Z}$ . Over here, we have $\mathfrak{a}_1$ divides $2\alpha$ , where $\alpha$ is in $\mathbb{Z}[i\sqrt{5}]$ , as opposed to being just in $\mathbb{Z}$ . Second, $\mathfrak{a}_1 \times \mathfrak{a}_3 = 1 + i \sqrt{5}$ , so $\mathfrak{a}_1$ also divides $1 + i \sqrt{5}$ , and hence divides $\beta(1 + i \sqrt{5})$ , where $\beta$ is some element of $\mathbb{Z}[i\sqrt{5}]$ . Adding the two pieces together, $\mathfrak{a}_1$ divides $2\alpha + \beta (1 + i \sqrt{5})$ (the sum of two multiples of $\mathfrak{a}_1$ is again a multiple of $\mathfrak{a}_1$ ).

Essentially, this means that $2\alpha + \beta (1 + i \sqrt{5})$ for each $\alpha, \beta \in \mathbb{Z}[i\sqrt{5}]$ is in $\mathfrak{a}_1$ ‘s version of $\mathbb{Z}[i\sqrt{5}]$ ! Or, writing it in terms of sets,

$\left\{2\alpha + \beta (1 + i \sqrt{5}) : \alpha, \beta \in \mathbb{Z}[i\sqrt{5}] \right\} \subseteq \langle \mathfrak{a}_1 \rangle,$

where we put those funny brackets around $\mathfrak{a}_1$ to denote its version of $\mathbb{Z}[i\sqrt{5}]$ – the set of its multiples.

But what is the set on the left really?

Well, it is just $2$ ‘s and $(1 + i \sqrt{5})$ ‘s version of $\mathbb{Z}[i\sqrt{5}]$ ! Using the funny brackets, we write

$\langle 2, 1 + i \sqrt{5} \rangle \subseteq \langle \mathfrak{a}_1 \rangle.$

After a bit of thinking, one realizes that the containment $\subseteq$ ought to be an equality $=$ : Indeed, if $\langle \mathfrak{a}_1 \rangle$ were any bigger, while still remaining a version of $\mathbb{Z}[i\sqrt{5}]$ , then it would actually be the whole of $\mathbb{Z}[i\sqrt{5}]$ – try seeing this yourself! That would then imply that $\mathfrak{a}_1$ would be a unit: $+1$ or $-1$ , but that would not solve our purpose: for then $\mathfrak{a}_2$ would have to be $\pm 2$ , which does not divide $1 - i \sqrt{5}$ ( $(1 + i \sqrt{5})/2$ is not in $\mathbb{Z}[i\sqrt{5}]$ ), meaning we don’t have a factorisation at all.

All in all,

$\langle \mathfrak{a}_1 \rangle = \langle 2, 1 + i \sqrt{5} \rangle.$

But, alas, as we already know, there is no single number whose version of $\mathbb{Z}[i\sqrt{5}]$ – the thing on the right – is $2$ ‘s and $(1 + i \sqrt{5})$ ‘s version of $\mathbb{Z}[i\sqrt{5}]$ – the thing on the left. Try spelling the details out: suppose that $\mathfrak{a}_1$ is really in $\mathbb{Z}[i\sqrt{5}]$ . Then use the divisibility relations that $\mathfrak{a}_1$ satisfies to show that it must be either $+1$ or $-1$ – but that would mean that its version of $\mathbb{Z}[i\sqrt{5}]$ is the whole thing, as we just discussed.

So, we must go one step further, dropping the bracket: $\langle \rangle$ , going from a number of a set, so that

$\mathfrak{a}_1 = \langle 2, 1 + i \sqrt{5} \rangle.$

It is because of the impossibility of writing the $\langle 2, 1 + i \sqrt{5} \rangle$ in the form $\langle \mathfrak{a}_1 \rangle$ for $\mathfrak{a}_1$ in $\mathbb{Z}[i\sqrt{5}]$ is why unique factorization fails for $6$ . Thus, the closest we can get is setting $\mathfrak{a}_1$ to be the whole set.

Notice that it is not just $2$ that is inside $\mathfrak{a}_1$ , but rather the whole of $2$ ‘s version of $\mathbb{Z}[i\sqrt{5}]$ – or $\langle 2 \rangle$ – that is inside $\mathfrak{a}_1$ . Recall that $\langle b \rangle \subseteq \langle a \rangle \implies a \mid b$ back in $\mathbb{Z}$ . So, we get a fleeting hint that since $\langle 2 \rangle \subseteq \langle 2, 1 + i \sqrt{5} \rangle$ , could we possibly have that the set $\langle 2, 1 + i \sqrt{5} \rangle$ divides the set $\langle 2 \rangle$ ? Well, then we must find $\mathfrak{a}_2$ such that

$\langle 2, 1 + i \sqrt{5} \rangle \times \mathfrak{a}_2 = \langle 2 \rangle,$

which is also going to be a set! What is $\mathfrak{a}_2$ ?

Well, in a similar way, one reasons out that

$\mathfrak{a}_2 = \langle 2, 1 - i \sqrt{5} \rangle$

(recall that this is just the set of all possible sums of a multiple of $2$ and a multiple of $1 + i \sqrt{5}$ in $\mathbb{Z}[i\sqrt{5}]$ ).

But then what is

$\langle 2, 1 + i \sqrt{5} \rangle \times \langle 2, 1 - i \sqrt{5} \rangle?$

What does it mean to multiply two sets?

We keep calm and use FOIL. More precisely, we just multiply a random element of the first set with another random element of the second set, and then do this for every pair of elements to get the product set.

Well, on the one hand, an element of the first set may be written as $2 \alpha + \beta (1 + i \sqrt{5})$ and an element of the second set may be written as $2 \gamma + \delta (1 - i \sqrt{5})$ for some $\alpha, \beta, \gamma, \delta \in \mathbb{Z}[i\sqrt{5}]$ . Multiplying everything out, the product is

$4 \alpha \gamma + 2 \beta \gamma + 2 \beta \delta + 2 \alpha \delta - 2 i \sqrt{5} (\alpha \delta + \beta \delta - \beta \gamma).$

Did you notice? It’s a $\mathbb{Z}[i\sqrt{5}]$ multiple of $2$ , since you can cleanly factor out a $2$ ! And you can go the other way as well, showing that every multiple of $2$ is of this form! In other words,

$\langle 2, 1 + i \sqrt{5} \rangle \times \langle 2, 1 - i \sqrt{5} \rangle = \langle 2 \rangle,$

and we have no difficulty in associating the right side with $2$ . After all, it is $2$ ‘s version of $\mathbb{Z}[i\sqrt{5}]$ ! So, while $2$ is irreducible as a plain number, it is not irreducible as a version of $\mathbb{Z}[i\sqrt{5}]$ .

We can apply the same line of reasoning to $3$ , to get that

$\langle 3, 1 + i \sqrt{5} \rangle \times \langle 3, 1 - i \sqrt{5} \rangle = \langle 3 \rangle.$

Now, watch what happens when we multiply $\langle 2, 1 + i \sqrt{5} \rangle$ and $\langle 3, 1 + i \sqrt{5} \rangle$ – you can try working through the product – we get $\langle 1 + i \sqrt{5} \rangle$ and we also have that

$\langle 2, 1 - i \sqrt{5} \rangle \times \langle 3, 1 - i \sqrt{5} \rangle = \langle 1 - i \sqrt{5} \rangle.$

Along the same lines, while $1 + i \sqrt{5}$ is irreducible as a plain number, it is not irreducible as a version of $\mathbb{Z}[i\sqrt{5}]$ !

What has this achieved? Well, clearly

$\langle 6 \rangle = \langle 2 \rangle \times \langle 3 \rangle = \langle 2, 1 + i \sqrt{5} \rangle \times \langle 2, 1 - i \sqrt{5} \rangle \times \langle 3, 1 + i \sqrt{5} \rangle \times \langle 3, 1 - i \sqrt{5} \rangle,$

and on the other side

$\langle 6 \rangle = \langle 1 + i \sqrt{5} \rangle \times \langle 1 - i \sqrt{5} \rangle = \langle 2, 1 + i \sqrt{5} \rangle \times \langle 3, 1 + i \sqrt{5} \rangle \times \langle 2, 1 - i \sqrt{5} \rangle \times \langle 3, 1 - i \sqrt{5} \rangle.$

We have recovered unique factorization! We just had to look beyond numbers and into some special sets.